零知识证明,from Zero to Hero
新年期间,笔者又重新发起对零知识证明的冲锋,因为就像 V 神说的「this stuff is genuinely hard」。作为非数学科班的笔者,第一次学习零知识证明的时候烧掉了 CPU 也才理解了最多五成,但是放弃可不是笔者的风格,在新年十天中花费了大半的有效精力重新学习零知识证明,最终有了一点浅薄的理解,在这里记录分享下。
从一个故事开始-神奇的山洞
相信每一个对零知识证明有简单了解的朋友都听说过这么一个故事:
Alice 和 Bob 来到一个山洞,山洞只有一个入口,山洞中有一个带密码的门,有两条路可以到达门,我们将两条路分别称为 C 和 D。
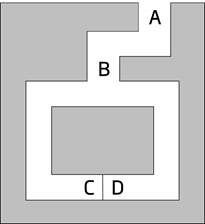
Bob 对 Alice 说他知道这扇门的密码,但是 Bob 又不想直接告诉 Alice 门的密码。那应该怎么办呢?
Alice 站在山洞的门口,让 Bob 随便选择一条路进入山洞内部。此时 Alice 不知道 Bob 选择了 C 还是 D 通道,然后 Alice 假设让 Bob 从 C 通道出来,并且此时 Bob 是从 D 通道进入,那么 Bob 只能穿过密码门,从而证明了 Bob 确实知道密码。
对于这样一次这样的行动,有 $\frac{1}{2}$ 的概率 Alice 要求和 Bob 进入的不是一个通道,也就是说有 $\frac{1}{2}$ 的概率 Bob 确实知道密码,那么当重复足够多的次数 n,Bob 靠运气才能出来的 $\frac{1}{2^n}$ 概率。通俗的就是说重复足够多的次数,Bob 向 Alice 证明了他确实知道这个密码,同时 Alice 也无法知道密码是什么。这也就是我们所说的零知识证明!
有什么意义-ZCash为例
回到现实,零知识证明究竟能够做什么,能够为我们带来什么,为什么它会受到 V 神的推崇称为区块链下一个十年的重要组成部分。
我们知道对于区块链,在链上所有的数据都可以被任何人查看,这点是去中心化的基础,但是同时也让隐私无法保证,任何一笔交易都能被知道,那么是否有一种方法能够进行链上行为的保密呢,这就是零知识证明的作用。
以 Zcash 这个著名的隐私币为例子,其交易过程类似比特币,一个比特币交易接受若干个输入 TI,同时产生若干个输出 TO,而尚未花出的 TO 就是 UXTO(Unspent Transaction Output) ,在这个过程中付款人会用自己的私钥进行签名验证自己确实拥有 UXTO,并且指定收款人的公钥从而保证只有收款人才能使用。
在 Zcash 中 UXTO 的概念被 note 替代 note=(PK, v, r) 其中 PK 是所有者的公钥,v 代表金额,r 代表唯一区分 note 的序列号。对于 Zcash 的隐藏地址交易情况,输入和输出都没有地址和金额,作为代替的是 note 的废弃通知和签发通知:
签发通知(note commitment):作为交易的输出,表示一张新 note 被签发。一个有效的 commitment 是一张 note 存在的证明,然而从它包含的信息中并不知道是哪张 note,也就无法知道所有者是谁,金额多少。为满足这一点,最简单的方法是对 note 的描述信息取哈希,因此 note 对应的 commitment 可以简单描述为 HASH(note);
废止通知(note nullifier):作为交易的输入,表示一张老支票将作废(
因为马上要被兑现、花掉了)。同比特币一样,一个交易的输入一定是另一个交易的输出,因此 nullifier 对应唯一一个 commitment(结合commitment的定义,也就唯一对应一张note),但从它包含的信息并不能推导出是哪个 commitment(如果可以的话,ZCash交易便可被追踪,因而丧失隐私性了)。为构造满足要求的 nullifier,取哈希依然是个好办法,因此序号为 r 的note,对应的 nullifier 可描述为 HASH(r)。
ZCash 的所有节点各自维护一个 nullifier 和 commitment 集合,随着交易的进行不断更新这个集合,我们看下面的例子,有三张 note,其中 note2 已经被花掉了。
| Commitment Set | Nullifier Set |
|---|---|
| C1 = HASH(note1) | NF1 = HASH(r2) |
| C2 = HASH(note2) | |
| C3 = HASH(note3) |
假设 Alice 拥有 note1,现在 Alice 想要转账给 Carl 金额 v1,Carl 的公钥是 PK4,现在 Alice 将执行以下步骤:
- 随机挑选一个序列号 r4,并以此产生 note4 = (PK4, v1, r4);
- 秘密地将 note4 发给 Carl;
- 将 note1 的nullifier,即 nf2 = HASH(r1),以及新产生的 note4 的 commitment,即其哈希值 HASH(note4) 广播给所有节点。
对于收到广播的节点,检查 nf2 是否存在于 nuffifier set 中,如果没有说明 nf2 对应的 note1 没有被花掉,即没有“双花”,然后将 HASH(note4) 的 commitment 以及 nf2 加入队列中。
| Commitment Set | Nullifier Set |
|---|---|
| C1 = HASH(note1) | NF1 = HASH(r2) |
| C2 = HASH(note2) | NF2 = HASH(r1) |
| C3 = HASH(note3) | |
| C4 = HASH(note4) |
现在就存在一些问题,例如 Alice 给出废弃的 nf2 对应的支票是否真实存在;nf2 对应的支票 Alice 是否有支配权(即 Alice 是否有 note 中公钥对应的私钥);
按照正常的逻辑 Alice 可以用自己的私钥签名来证明自己确实有 note 的支配权,但是这就暴露了是 Alice (这里不是指 Alice 的现实世界身份,而是其地址)。那么应该如何做呢?零知识证明在这里就要大展身手了!Alice 会提供一个证明 π。π 足以证明Alice 知道能满足以下条件的PK1,SK1(PK1对应的私钥)和 r1 的值:
- 用PK1、r1 复原的 note 数据结构,其哈希值存在于 commitment 集合中 → 用以支付的 note 是有效的;
- SK1 是 PK1的私钥 → Anna有权使用这张 note;
- HASH(r1) = NF2 → nullifier 与 commitment 一致,花费的确实是 note1。
在其他节点验证通过 π 后,这次交易才是合法的。我们稍微提前揭露点零知识证明的基本特征:
完备(complete):若一个证明方确实掌握了某论断的答案,则他肯定能找到方法向验证方证明他手中掌握的数据的正确性,也就是“真的假不了”。
健全(sound):若一个证明方完全不掌握某论断的答案,则他无法(或只能以极低概率)说服验证方相信他手中所谓答案的准确性,也就是“假的真不了”。
零知识(zero-knowledge):验证方除了知道证明的结果外,对其他信息一无所知。
那么接下来我们就开始正式揭开零知识证明的神秘面纱,以 zk-SNARK 协议进行分析。
zk-SNARK
zk-SNARK 全名 Zero-knowledge succinct non-interactive arguments of knowledge,其中名称中各个部分的含义:
- zero-knowledge:零知识,即验证方无法从证明中提取除了证明本身的其他知识
- succinct:简洁
- non-interactive:非交互式
我们先不考虑上文中 ZCash 的证明需求,因为这太复杂了。我们首先思考在山洞的故事中,各个部分的抽象含义:
- 山洞的环境:这是条件约束
- Alice 提出质询要求:发起验证问题
- Bob 给出结果:求解答案
有约束,有问题,有解这让我们能够联想到什么数学概念,对就是函数计算!让我抽象看下:
- prover 声明它知道函数 $f(x)$,想要让 verifier 相信
- verifier 挑选随机值 $m$,对于 $g_a=f(m)$,,自本地计算出 $g_a$,同时将 $m$ 传递给 prover。
- prover 使用 $m$ 计算出来结果 $g_b=f’(m)$ 传回给 verifier,verifier 比较 $g_a$ 是否等于 $g_b$。如果相等,声明的可信度增加。
- 重复 2-3 过程 n 轮都通过验证,那么 prover 的函数「大概率」 $f’(x)$ 确实是 $f(x)$,也就是 prover 确实知道函数 $f(x)$。
当然这个过程现在看来十分的弱并且麻烦,比如 Alice 也需要知道 $f(x)$;Bob 假如不使用给定值 m 或者 $f’(x)$ 只是在 m 时才等于 $f(x)$;验证轮次过多等等问题。接下来我们逐步的完善并增强我们的协议。
多项式
首先对于上述过程中的函数,我们想要寻找一个合适的,我们来看一个例子:
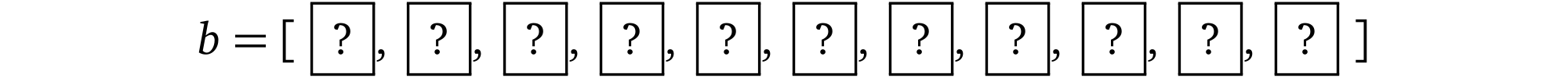
对于一个 10 位的数组,prover 声称每一位都是 1,verifier 一次只能读一位,按照一定顺序进行检查,第一次抽样结果为 1,「陈述」的可信度为 $\frac{1}{10}$ ,如果需要 50% 的可信度最少执行 5 次校验,如果数组元素超过百万个,那么校验次数也将爆照,效率极低,所以这种验证方式是不可行的。
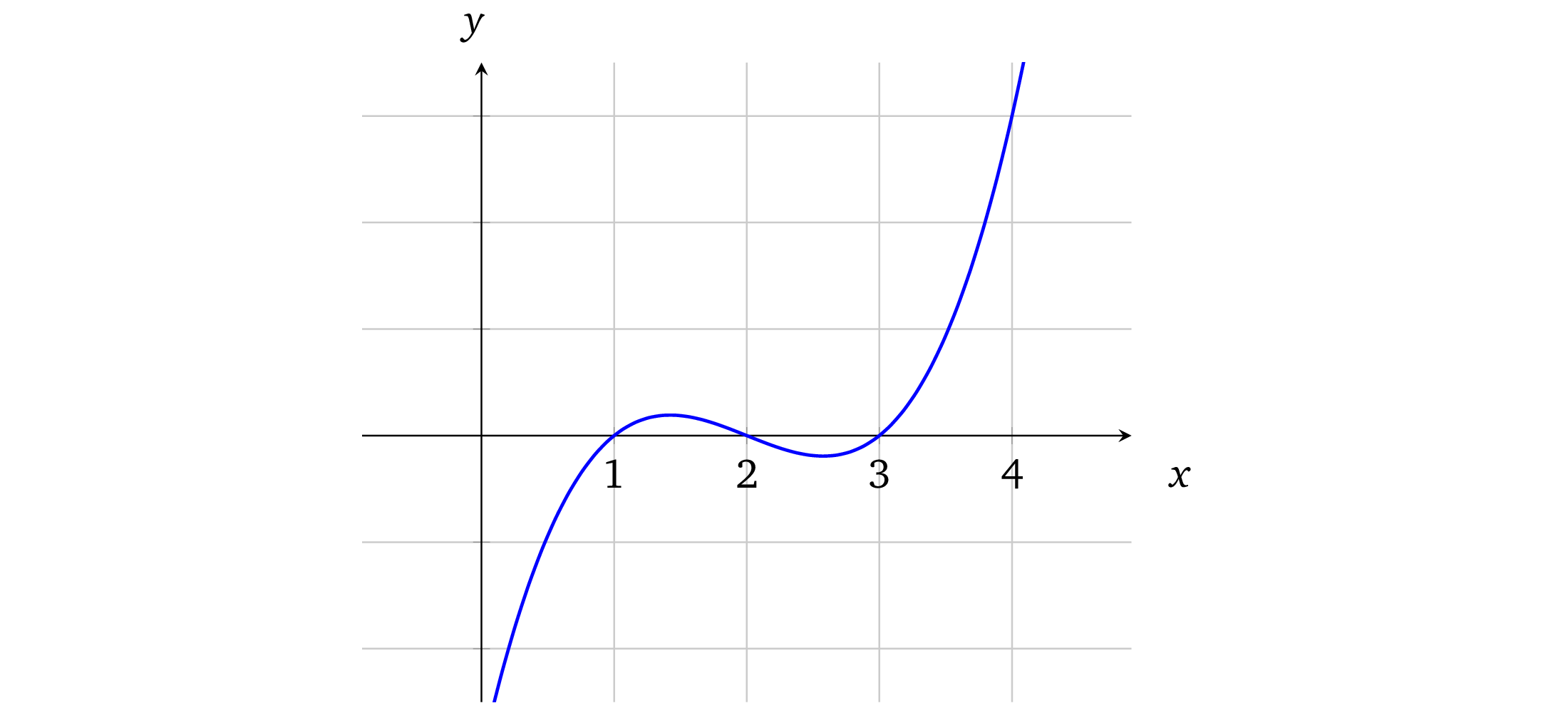
对于多项式有一个很好的性质:一个阶数为 d 的多项式至多有 d 个解。因此任何多项式在任意点的计算结果都可以看做是唯一身份的表示,即一个点 x 对应一个 y 值,因为在 x 取值范围足够大的情况下,最多有 d 个点对应同一个 y 值。
有了这个性质,我们再看 prover 声称他知道一些 verifier 也知道的多项式:
- verifier 选择一个随机值 x 并在本地计算多项式结果
- verifier 将 x 值给到 prover,并让他计算相关的多项式结果
- prover 代入 x 到多项式计算并将结果给到 verifier
- verifier 检查本地的计算结果和 prover 的计算结果是否相等,如果相等那就说明 prover 的陈述具有较高的可信度
我们把 x 的取值范围定在 1 到 $10^{77}$,那么计算结果不同的点的数量,就有 $10^{77}-d$ 个。因而 x 偶然撞到这 d 个结果相同的点中任意一个的概率就等于(可以认为是几乎不可能):$\frac{d}{10^{77}}$。由此简化了需要 n 轮验证过程。
然后对于多项式,「知道多项式」代表知道多项式每个幂的「系数」,例如对于:$c_1x^1+c_0=0$ 知道这个多项式代表他知道 $c_0,c_1$
现在我们整个协议就是围绕着多项式开始进行不断完善。
因式分解
代数的基本定理表明了任意的一个多项式只要它有解,就可以将它分解成线性多项式(即,一个阶数为 1 的多项式代表一条线),因此,我们可以把任意有效的多项式看成是其因式的乘积:
$$
(x-a_0)(x-a_1)…(x-a_n)=0
$$
也就是说如果任意一个因式为 0,那么整个等式都为 0,也就是说式子中所有的 $a_s$ 就是多项式的所有解。例如:
$$
x^3−3x^2+2x=(x−0)(x−1)(x−2)
$$
我们将要证明的多项式记作 $p(x)$,将多项式的解记作 $t(x)$,那么一定存在某个多项式 $h(x)$,使得 $p(x)=h(x)·t(x)$,即 $h(x)=\frac{p(x)}{t(x)}$。例如 $p(x)=x^3-3x^2+2x$ 除以 $t(x)=(x-1)(x-2)=x^2-3x+2$,得到结果 $x$,可以看到没有余数。
$$
\require{enclose}
\begin{array}{r}
\phantom{x+1}x \
x^2 - 3x + 2
\enclose{longdiv}{x^3 - 3x^2 + 2x} \
\underline{-x^3 + 3x^2 - 2x} \
\phantom{x^2 - 3x + 2}0
\end{array}
$$
如果 prover 无法找到 $h(x)$ 满足上述条件,那么通过 $\frac{p(x)}{t(x)}$ 得到的一定会有余数,例如 $p’(x)=2x^3-3x^2+2x$,计算出来的$h(x)=2x+3+\frac{7x−6}{t(x)}$,有极低的概率 $\frac{7x−6}{t(x)}$ 是可以整除的。但是着要求检查多项式系数也是整数,$p$ 和 $h$ 也是整数,会对协议产生很大的限制。
现在我们的协议可以转换为下面:
- verifier 挑选一个随机值 $r$, 计算 $t = t(r)$ (即,求值) ,然后将 $r$ 发送给 prover。
- prover 计算 $h(x)=\frac{p(x)}{t(x)}$ ,并对 $p(r)$ 和 $h(r)$ 进行求值,将计算结果 $p$, $h$ 提供给 verifier。
- verifier 验证 $p= t⋅h$,如果多项式相等,就意味着 $t(x)$ 是 $p(x)$ 的因式。
那么为什么要这么做因式分解转换协议的证明呢呢?可以看到现在 verifier 不需要知道完整的 $p(x)$,就能进行校验,一定程度上实现了「零知识」。
但是现在存在一些问题:
- prover 可能并不知道他所声称的 $p(x)$,他可以先算一下 $t = t(r)$,然后选择一个随机值 $h$,由此计算出 $p = t⋅h$。因为等式是成立的,所以也能通过 verifier 的校验。
- 因为 prover 知道随机点 $x = r$ ,他可以构造出一个任意的多项式,这个任意多项式与 $t(r) ⋅ h(r)$ 在 $r$ 处有共同点。
这都是因为暴露的原始值 $r$ 所导致的,让 prover 能够知道 $r$ 和 $t(r)$,那么有没有一种方法不让 prover 知道原始值同时也能完成计算呢?
模糊计算
同态加密
常见的同态加密有整数幂取模,椭圆曲线倍乘等,这里以整数幂取模为例子:
总体思路就是我们选择一个基础的(基数需要具有某些特定的属性)的自然数 $g$(如 5),然后我们以要加密的值为指数对 $g$ 进行求幂。例如,如果我们要对 3 进行加密:
$$
5^3=125
$$
这里 125 就是 3 对应的密文。如果我们想要对被加密的值乘 2,我们可以以 2 为指数来对这个密文进行计算。
$$
125^2=15625=(5^3)^2=5^{2×3}=5^6
$$
我们不仅可以用 2 来乘以一个未知的值并保持密文的有效性,还可以通过密文相乘来使两个值相加,例如 3+2:
$$
5^3⋅5^2=5^{3+2}=5^5=3125
$$
同样的,我们还可以通过相除提取加密的数字,例如:5-3
$$
\frac{5^5}{5^3}=5^5⋅5^{−3}=5^{5−3}=5^2=25
$$
不过由于基数 5 是公开的,很容易就可以找到被加密的数字。只要将密文一直除以 5,直到结果为 1,那么做除法的次数也就是被加密值的数。
模运算
这里就到了模运算发挥作用的地方了。模运算的思路如下:除了我们所选择的组成有限集合的前 n 个自然数(即,0,1,…,$n-1$)以外,任何超出此范围的给定整数,我们就将它“缠绕”起来。例如,我们选择前六个数。为了说明这一点,可以把它看做一个有六个单位大小相等刻度的圆;这就是我们所说的范围(通常指的是有限域)。

现在我们看一下数字八应该在哪里。打个比方,我们可以把它看成一条长度为 8 的绳子。

如果我们将绳子固定在圆圈的开头
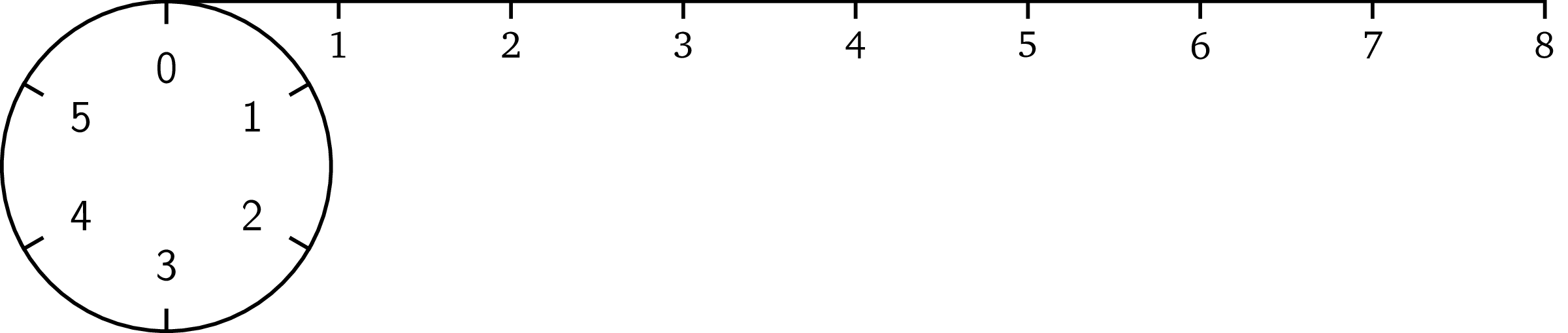
然后用绳子缠绕圆圈,我们在缠完一圈后还剩下一部分的绳子。

然后我们继续缠绕,这根绳子将在刻度 2 的地方终止。

这就是模运算操作的结果。无论这根绳子多长,它最终都会在圆圈一个刻度处终止。因而模运算结果将保持在一定范围内(例子中是 0 到 5)。长度为 15 的绳子将会在刻度 3 的地方终止,即 6 + 6 + 3 (缠 2 个完整的圈并剩下 3 个单位长的部分)。负数运算类似,唯一不同的地方就是它是沿相反方向缠绕的,如 -8 的取模结果是 4。
我们执行算术运算,结果都将落在这 n 的范围内。现在开始我们将用符号 “mod n” 来表示这个范围内的数。
$$
3×5 = 3\ mod\ 6 \
5+2 = 1\ mod\ 6
$$
另外,模运算最重要的性质就是运算顺序无所谓。例如,我们可以先做完所有的操作,然后再取模,或者每操作完一步都去取模。例如 $(2 × 4 – 1) × 3 = 3 (mod\ 6)$ 就等于:
$$
2 × 4 = 1\ mod\ 6 \
2 - 1 = 1\ mod\ 6 \
1 × 3 = 3\ mod\ 6 \
$$
那么模运算到底有什么用呢?就是如果我们使用模运算,从运算结果再回到原始值并不容易,因为很多不同的组合会产生一个同样的运算结果:
$$
5 × 4 = 2\ mod\ 6\
4 × 2 = 2\ mod\ 6\
2 × 1 = 1\ mod\ 6\
$$
没有模运算的话,计算结果的大小会给找出原始值提供一些线索。除非这里既能把信息隐藏起来,又可以保留常见的算术属性。
事实上,如果模取得相当大,从运算结果倒推指数运算就不可行了;现代密码学很大程度上就是基于这个问题的“困难”。方案中的所有同态性质都保留下来了:
$$
encryption:5^3=6(mod\ 7)\
multiplication:6^2=(5^3)^2=5^6=1(mod\ 7)\
addition:5^3·5^2=5^5=3(mod\ 7)
$$
也就是说我们的加密函数可以表示为:$E(v)=g^v(mod\ n)$
注意1:这里的乘法只能是「加密值」乘「未加密值」,两个加密值是无法直接做乘法的
加密多项式
现在我们继续调整协议,因为同态加密并不允许再对加密值求幂(根据上述的加密值不能做乘法),那么对于例子 $p(x)=x^3-3x^2+2x$ 需要依次计算出 $x$ 每个幂的取值:$E(x),E(x^2),E(x^3)$。那么对于阶数为 $d$ 的多项式:
Verifier
- 取一个随机数 $s$ ,也就是秘密值
- 指数 $i$ 取值为 0,1,…,$d$ 时分别计算对 $s$ 求幂的加密结果,即:$E(s^i)=g^{s^i}$
- 代入 $s$ 计算未加密的目标多项式:$t(s)$
- 将对 s 求幂的加密结果提供给 prover:$E(s^0),E(s^1)…E(s^d)$
Prover
计算多项式 $h(x)=\frac{p(x)}{t(x)}$
使用加密值 $g^{s^0},g^{s^1},…g^{s^d}$ 和系数 $c_0,c_1,…c_n$ 计算 $E(p(s))=g^{p(s)}=(g^{s^d})^{c_d}…(g^{s^1})^{c_1}*(g^{s^0})^{c_0}$
然后同样计算 $E(p(s))=g^{h(s)}$
将结果 $g^p$ 和 $g^h$ 提供给 verifier
Verifier
- 最后一步是 verifier 去校验 $p=t(s)·h:g^p=(g^h)^{t(s)}=>g^p=g^{t(s)·h}$
prover 不知道随机值 $s$,无法得到 $t(s)$,所以他很难提出 $h(s)$ 使得 $E(p(s))=E(h(s)·t(s))$。
但是这里还有另一个问题,比如 prover 知道另一个题目满足 $p’(x)=h’(x)·t(x)$,通过计算 $p’(n)$ 和 $h’(n)$ 发送给 verifier 同样能够通过验证,但是 prover 其实知道的是另一个「题目」的答案,并非 verifier 关心的 $p(x)=h(x)·t(x)$。
多项式限制(KCA)
我们想要限制 prover 使用 verifier 提供的加密值 $E(s^i)$,而不是使用其他值来带入计算,这里可以使用类似「校验和」的方式。
Alice 有一个值 $a$,她想要 Bob 对其进行任意指数的求幂(这里 $a$ 是一个有限域群的生成器),唯一的要求是只能对 $a$ 进行求幂,为了保证这一点,她要:
选择一个随机数 $α$
计算 $a’=a^α(mod\ n)$
提供一个元组 $(a, a’)$ 给 Bob, 然后让他对这两个值执行任意的求幂运算,返回结果元组 $(b, b’)$,这里的指数 “$α$-变换” 依然保持不变,即 $b^α = b’(mod\ n)$
因为 Bob 无法从元组 $(a, a’)$ 中提取 $α$ 的值,通过暴力破解也难以实现,那就可以推断 Bob 生成有效元组的唯一方法就是执行下面的步骤:
选择一个值 $c$
计算 $b=(a)^c(mod\ n)$ 和 $b’ = (a’)^c (mod\ n)$
回复 $(b,b’)$
有了回复的元组和 α,Alice 就可以验证等式:
$$
(b)^α = b’\
(a^c)^α = (a’)^c\
a^{c·α} = (a^α)^c
$$
结论是:
- Bob 在元组的两个值的计算上都用了同一个指数(即 $c$)
- Bob 只能用 Alice 原本的元组来保持 α 关系
- Bob 知道指数 $c$,因为构造验证值 $(b,b′)$ 的唯一方式是用同一个指数
- Alice 并不知道 $c$,这和 Bob 不知道 $α$ 的原因一样
- 虽然 $c$ 是被加密的,但它的可能取值范围并不足够大到保持其零知识的性质,这个问题我们将在后面“零知识”那一节解决。
现在可以调整协议增加一个验证项:
- verifier 提供加密值 $g^{s^i}$ 和对应的变换 $g^{αs^i}$
- prover
- 计算 s 幂的加密多项式:$g^{p(s)}=(g^{s^0})^{c_0}·(g^{s^1})^{c_1}…(g^{s^d})^{c_d}=g^{(c_0s^0+c_1s^1+…+c_ds^d)}$
- 计算 s 幂的「校验」加密多项式:$g^{αp(s)}=(g^{αs^0})^{c_0}·(g^{αs^1})^{c_1}…(g^{αs^d})^{c_d}=g^{(c_0αs^0+c_1αs^1+…+c_dαs^d)}$
- 将计算结果 $g^p,g^{p’}$ 给回 verifier
- verifier 校验:$(g^p)^α=g^{p’}$
现在我们就可以确保 prover 是用了 verifier 提供的多项式而不是其它值做计算的了,因为别的方法不能够保持 $α$ 变换。
同样的为了不让 verifier 从 prover 提供的数据中提取出多余的知识,我们也可以对 $g^p,g^{p’},g^h$ 做类似的 $α$ 变换
配对(双线性映射)
在同态隐藏中,是一对一的关系,是将一个输入到一个输出,双线性映射则是将两个元素映射到另一个域的第三个元素中,同时在两个输入上都具备线性:
$$
e(P+R,Q)=e(P,Q)+e(R,Q)\
e(P,Q+S)=e(P,Q)+e(P,S)
$$
那么假设对于 $x$ 的任意两种因数分解 $(a,b)$ 和 $(c,d)$,存在两个加法同态映射 $E_1$ 和 $E_2$,以及一个双线性映射 $e$,使得以下等式总是成立
$$
e(E_1(a),E_2(b))=e(E_1(c),E_2(d))=X
$$
那么,对于 $x\rightarrow X$ 的映射也是加法同态映射的,记作 $E$。
证明:
$$
E(ax_1+bx_2)\
=e(E_1(ax_1+bx_2),E_2(1))\
=e(aE_1(x_1)+bE_1(x_2),E_2(1))\
=ae(E_1(x_1),E_2(1))+be(E_1(x_2),E_2(1))\
=aE(x_1)+bE(x_2)
$$
- 第一步:根据 $ax_1+bx_2=(ax_1+bx_2)*1$ ,基于假设的等式 $e(E_1(c),E_2(d))=X$ 推导出来
- 第二步:因为 $E_1$ 是加法同态映射,所以 $E_1(ax_1+bx_2)=aE_1(x_1)+bE_1(x_2)$
- 第三步:根据双线性映射在两个输入上都具备线性的性质可以推出,$e(P+R,Q)=e(P,Q)+e(R,Q)$
- 第四部:根据假设 x 的因式分解可以推出,$e(E_1(x_1),E_2(1))=E(x_1)$
- 最后得到了对于运算 $E$ 得到 $E(ax_1+bx_2)=aE(x_1)+bE(x_2)$ 这就是加法同态映射。
最终我们可以得到一个这个:$E(xy)=e(E_1(x),E_2(y))$,可以看到我们利用配对 $e$ 使加法同态加密的 $x,y$ 映射到了另一个加法同态加密 $E$ 并且获得了 $xy$ 乘法形式的运算。
有了这个工具,在后续中我们就可以处理需要两个加密值相乘的问题了。
非交互式
我们注意到协议的过程中 verifier 需要先将众多加密参数传递给 prover,对于 ZCash 这将高达数百万个,每次验证都需要传输会非常麻烦,并且 verifier 可以和 prover 串通告诉密码参数 $s, α$ 来作弊,那么如何解决呢?我们可以通过某种方式,提前生成一个可以被重复使用,公开,可信,又不会被滥用的秘密参数参数,在所有的验证过程中,就不需要 verifier 去质询,只需要 prover 去验证即可,我们把这些「共同参考数据集」称为 CRS(Commen Reference String)。
这里简单介绍一个方案
首先我们让一个诚实的参与方生成密码值 $s$ 和 $α$,然后 $α$ 和所有必要的 $s$ 的幂以及对应的 $α$-变换都被加密后,原始数据就需要删除掉:
$$
g^α,g^{s^i},g^{αs^i}
$$
这也就是我们所说的 CRS。把 CRS 分成两组,并添加一个 $g^{t(s)}$ (其实这个值不重要),用于后续协议使用:
- proving key:$(g^{s^i},g^{αs^i})$
- verification key:$(g^{t(s)},g^α)$
但是对于其他节点就需要信任这个生成者确实删除了 $α$ 和 $s$,其中一种解决方案是多个参与方合作生成一个组合式的 CRS,这样单独的参与者就不知道「秘密」了。我们假设有三个参与者 Alice,Bob 和 Carol ,对应为 A,B 和 C,其中 $i$ 为 $1, 2, …, d$:
Alice 选择随机数 $s_A$ 和 $α_A$,然后公开她的 CRS:
$$
(g^{s^i_A}, g^{α_A}, g^{α_As^i_A})
$$Bob 选择他的随机数 $s_B$ 和 $α_B$,然后通过同态乘法结合 Alice 的 CRS:
$$
((g^{s^i_A})^{s^i_B},(g^{α_A})^{α_B},(g^{α_As^i_A})^{α_Bs^i_B})=(g^{(s_As_B)^i},g^{α_Aα_B},g^{α_Aα_B(s_As_B)^i})
$$
然后 Bob 公开两方 Alice-Bob 的 CRS 结果:
$$
(g^{s^i_{AB}}, g^{α_{AB}}, g^{α_{AB}s^i_{AB}})
$$Carol 用她的随机值 $s_C$ 和 $α_C$ 做同样的事情公布 Alice-Bob-Carol 的 CRS
$$
(g^{s^i_{ABC}}, g^{α_{ABC}}, g^{α_{ABC}s^i_{ABC}})
$$
最后我们得到了混合的 $s^i$ 和 $α$:
$$
s^i=s^i_As^i_Bs^i_C,α=α_Aα_Bα_C
$$
现在只要有一个参与者是诚实的,就没有办法伪造证明。
现在还存在一个问题是验证参与者在生成 CRS 时的随机值时一样的,因为攻击者可以生成多个不同的随机值 $s_1,s_2,…$ 和 $α_1,α_2,…$ 然后将其带入 $s$ 的不同次幂计算,即不同次幂使用不同的 $s$ 和 $a$ ,从而使 CRS 无效或者不可用。
我们可以使用配对来乘以加密值,所以我们就可以从第一个参数开始逐一执行一致性校验,并且确保了每个参数都源于前一个。
我们用 s 的 1 次幂作为标准来校验每一个其它次幂的值与之是否保持一致,以下公式因为加密配对成立
$$
e(g^{s^i}, g) = e(g^{s^1}, g^{s^{i-1}})\forall i \in {2, \ldots, d}
$$
那么例如校验:- 2 次幂:$e(g^{s^2},g)=e(g^{s^1},g^{s^1})=>e(g,g)^{s^2}=e(g,g)^{s^{1+1}}$ 已知 $g^{s^1}$ 来带入公式校验 $g^{s^2}$
- 3 次幂:$e(g^{s^3},g)=e(g^{s^1},g^{s^2})=>e(g,g)^{s^3}=e(g,g)^{s^{1+2}}$ 同理
同理对于 α 变换也是成立
还有一个问题是如果一个攻击者是链上的最后一个参与者,他可以像链上的第一个参与者一样忽略前面的 CRS 随便构造一个有效的 CRS,这样他就变成了唯一一个知道秘密 $s$ 和 $α$ 的人。
为了解决这个问题,我们可以额外再要求除了第一个以外的每一个参与者去加密然后公开他的参数。例如,Bob 同样公开了
$$
(g^{s^i_B},g^{α_B},g^{α_Bs^i_B})\forall i \in {2, \ldots, d}
$$
这就可以去验证 Bob 的 CRS 是乘以了 Alice 的参数后正常获得的
- $e(g^{s^i_{AB}},g)=e(g^{s^i_A},g^{s^i_B})$
- $e(g^{α_{AB}},g)=e(g^{α_A},g^{α_B})$
- $e(g^{α_{AB}s^i_{AB}},g)=e(g^{α_As^i_A},g^{α_Bs^i_B})$
类似的 Carol 也要类似的给出并能证明她的 CRS 是乘以了 Alice-Bob 的 CRS 后获得的。
回顾协议架构
现在回顾我们的整个协议,已经是一个比较完善的证明
- Setup
- 挑选随机值 $s,α$
- 计算加密值 $g^α$ 和 ${g^{s^i}}{i\in[0,\ldots,d]}$,${g^{αs^i}}{i\in[0,\ldots,d]}$
- 生成 proving key:$({g^{s^i}}{i\in[d]}$,${g^{αs^i}}{i\in[d]})$
- 生成 verification key:$(g^α,g^{t(s)})$
- Proving
- 分配系数 ${c_i}_{i\in{0,\ldots,d}}$ (即知识) 得 $p(x)=c_dx^d+\ldots+c_1x_1+c_0x^0$
- 求多项式 $h(x)=\frac{p(x)}{t(x)}$
- 代入 ${g^{s^i}}_{i\in[d]}$ 计算多项式 $g^{p(s)}$ 和 $g^{h(s)}$ 的值
- 代入 ${g^{αs^i}}_{i\in[d]}$ 计算变换多项式 $g^{αp(s)}$ 的值
- 选择随机数 $δ$
- 构造随机化的证明 $π=g^{δp(s)},g^{δh(s)},g^{δαp(s)}$
- verification
- 映射证明 $π$ 为 $(g^p,g^h,g^{p’})$
- 验证多项式约束:$e(g^{p’},g)=e(g^p,g^α)$
- 验证多项式系数:$e(g^{p},g)=e(g^{t(s)},g^h)$
整个零知识的架构就类似上述,对于一阶约束系统(L1CS),矩阵向量的转换都是为了方便计算,本文已经足够长了,在未来可能会再做补充,相信看到这里的读者也能基本长舒一口气了。
总结回顾
洋洋洒洒近万字的文章,感谢前人的分析与介绍,这里笔者终于暂时啃下这块「硬骨头」,能够自闭环的说清楚什么是零知识证明,以及其大概的数学原理,这种将密码学与计算机工程巧妙结合的设计当真是一件美丽的艺术品!